Featured image: Structure of the Universe. NASA, ESA, and E. Hallman (University of Colorado, Boulder), Public domain, via Wikimedia Commons

Cosmic origami, the idea that the universe resembles an intricate origami sculpture, provides a novel way to visualize the large-scale structure of the cosmos. When viewed on grand scales, galaxies exhibit a stunning web-like pattern – almost like someone folded a flat sheet of dark matter into an ornate paper form. Clusters, filaments and sheets of galaxies surround voids, spanning hundreds of millions of lightyears.

While first glimpsed in early galaxy surveys, modern sky surveys like the Sloan Digital Sky Survey have mapped this cosmic origami in extraordinary detail. Simulations based on current cosmology can recreate these elaborate origami-like patterns from simple initial conditions after the Big Bang. However, the intricate physics involved in shaping cosmic origami’s web from an originally near-uniform matter distribution remains an active area of research.

An intriguing way to understand the formation of the cosmic web is through an analogy with the art of origami. In this view, the unseen distribution of dark matter that drives the evolution of large-scale structure can be envisioned as a three-dimensional manifold that over time gets folded, bent, and twisted by the gravitational forces arising from very slight primordial irregularities. The complex patterns created are reminiscent of an origami model folded from a flat sheet of paper.

Dr. Mark Neyrinck at Johns Hopkins University explored this “origami approximation,” noting similarities such as the tendency for matter to collapse along preferred directions, forming effectively one-dimensional filaments and two-dimensional walls where the manifold folds and intersects itself. The origami analogy provides an intriguing conceptual framework for visualizing the complex non-linear processes that mold dark matter into the cosmic web.

Cosmic Origami in 2D

The most straightforward origami model for the cosmos treats the folding dark matter sheet as two-dimensional like a sheet of paper being folded in three dimensions. Simple fold lines can produce idealized structures reminiscent of the Zel’dovich “pancakes” that are thought to form early on in cosmic structure formation. These pancakes are flattened regions where the sheet has collapsed along one dimension under gravity. The fold lines delineate collapsed walls and voids, in a pattern that can be folded up from an initially flat 2D manifold.

More intricate origami tessellations with nested structures have been designed to mimic the web-like patterns of filaments and nodes observed in galaxy surveys. This strictly 2D approach does not capture the full complexity of structure formation in the real 3D universe. Still, it provides a useful conceptual picture of how pancaking and collapse lead to a geometric partitioning of space into voids, walls, filaments, and nodes in a way that recalls folding a flat paper sheet.

Crease patterns that fold up into repeating polygon structures mimic the foam-like patterns of the cosmic web. For example, a Voronoi tessellation folding from a 2D sheet produces convex polygonal voids resembling those observed in galaxy surveys. The boundaries between voids map to filaments and walls where the sheet folds up.

These origami models are visually evocative and highlight geometrical principles like the tendency for matter to flow away from voids and collapse along preferred directions. However, since the sheet cannot stretch, the structures and their connectivity have some idealized limitations. For instance, all voids must be convex polygons in this case. The strict 2D approach also does not capture the intricate multi-stream flows and evolution of true 3D collapse. So while 2D origami tessellations provide a good conceptual representation, capturing the full dynamics of the cosmic web requires extending origami concepts to fold a 3D manifold.

Folding up the Universe in 3D

To capture the three-dimensional dynamics of the universe more accurately, Dr. Neyrinck proposed folding a 3D manifold representing the dark matter distribution in 6 dimensions – 3 for position and 3 for velocity. This dark matter sheet is envisioned to be initially flat, with near-zero velocities. Over time, gravity distorts the sheet, folding it up in position-velocity phase space. When projected down to 3D position coordinates, this folding creates the cosmic web pattern with its walls, filaments, and cluster nodes.

The principles of origami can be extended to this 3D context by considering folds along planes rather than lines. The flat-foldability constraints of paper origami also inspire geometrical constraints for folding a 3D manifold. This origami approximation provides a richer dynamical model for the formation of cosmic structures, able to represent simultaneous collapse along multiple axes. The folded sheet geometrically partitions phase space into streams, with boundaries called caustics delineating differences in sheet orientation. This helps visualize the multi-stream flows of real large-scale structure formation.

A key innovation of 3D origami models is representing the simultaneous collapse of matter along multiple axes into walls, filaments, and clusters. In 2D, origami folds model “polygonal collapse” as matter flows into pancakes and nodes. The 3D version is “polyhedral collapse” – matter flows along planes, collapsing polyhedral nodes tied together by filaments.

Unlike ideal spherical collapse, the facets of polyhedral collapse preferentially orient along the edges and vertices of the initial Cubic dark matter lattice. This leads to the coordinated formation of clusters, filaments, and walls observed in simulations and surveys. Polygonal collapse also naturally imparts angular momentum to galaxies forming at the nodes. The geometry of polyhedral collapse constrains the angles between adjoining filaments and the rotation of neighboring nodes. So 3D origami concepts like polygonal and polyhedral collapse capture some of the key physics involved in the hierarchical formation of cosmic structure from an initially smooth 3D distribution.

These geometrical 3D origami ideas can be illustrated through crease patterns that fold up into an idealized cosmic web. For instance, one can create a sectional Voronoi tessellation to represent the initial 3D distribution of dark matter. Origami folds are then delineated by the boundaries between Voronoi cells. As this crease pattern is folded upward, the cells deform into polygons, modeling polyhedral collapse into walls, filaments, and clusters. Adjacent facets of the collapse pattern adhere together, mimicking how streams of matter merge in overdense regions.

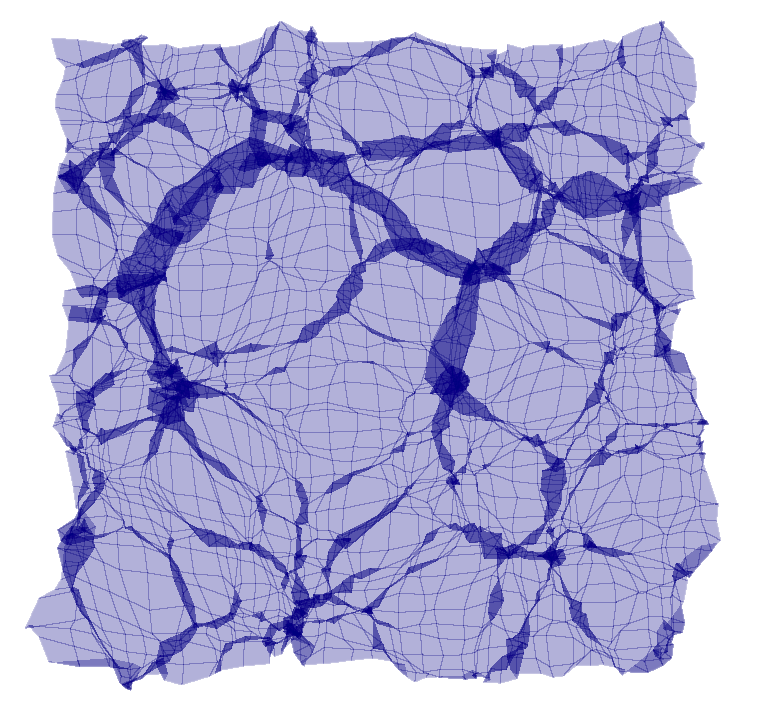
The result is a neatly folded geometric origami cosmic web. More complex patterns can be designed with different polygonal void shapes and connectivity to represent web-like structures. While abstract, these hands-on models clearly show how matter can flow from voids and collapse anisotropically to form elegantly intertwined structures through origami-like folding.

Beyond 3D: Origami in Higher Dimensions

The origami approximation can be taken a step further by considering how a 3D manifold could be folded in a higher dimensional hyperspace. At University of Brasília, we have extended mathematical origami to model folding a 3D “sheet” within a 4D or higher hyperspace by folding along planes rather than lines. This leads to a set of more varied and complex folds than are possible with a 2D sheet of paper. We have analyzed the geometry of these fold operations, which involve satisfying incidence constraints between points, lines, and planes via the folding plane. This exploration of “3D origami” provides tools to conceptualize the manifold of dark matter folding in perhaps 8 or more dimensions, as velocities, orientations, and other degrees of freedom come into play.

To understand how these 3D origami principles could apply to cosmic structure formation, consider a cubic 3D slice of the universe, perhaps 100 million lightyears on a side. The initial positions of dark matter particles in this slice could be mapped onto a 3D cubic lattice. Using the elementary 3D origami folds, we could then model the gravitational collapse of this slice into a network of clusters, filaments, and walls, as a step-by-step sequence of folds. This offers a novel hands-on way to geometrically model the complex multi-dimensional dynamics of structure formation.

Conclusions

While an idealized picture, the origami viewpoint illuminates geometrical principles sculpting the universe on its largest scales. Origami models make clear how voids evacuate matter to then intricately collapse into salient one- and two-dimensional structures tied together in a web-like network. Extending origami to fold 3D and higher-dimensional manifolds offers mathematical tools for analyzing the manifold’s complex phase-space contortions and dynamics.

So while the cosmic web may be not literally folding itself up like a work of paper art, thinking in terms of cosmic origami can provide intuitive and geometrical insights into the emergence of universal patterns. This elegant approximation captures key aspects of the continuous kneading and molding of matter into an intricately interconnected web of walls, filaments and clusters through the dynamic origami of gravity.