Origami has long been admired for its geometric elegance and artistic beauty. But who would have thought that this traditional craft holds the key to unlocking the secrets of universal computation? In a recent study, mathematicians Inna Zakharevich, at Cornell University, and Thomas Hull, at Franklin & Marshall College, have demonstrated that origami is “Turing complete” – capable of performing any computation, no matter how complex, that can be described algorithmically.

This revelation invites us to rethink the very nature of computation, blurring the boundaries between art and science. It’s a testament to the power of interdisciplinary exploration and a reminder that the path to innovation often lies in unexpected places.

Understanding Turing Completeness

To grasp the significance of this discovery, we must first understand the concept of Turing completeness. In 1936, the British mathematician Alan Turing proposed a theoretical model of computation consisting of an infinite tape divided into cells, each containing a symbol (e.g., 0 or 1). A tape head reads and writes these symbols, moving left or right, guided by a set of rules that dictate its actions based on the current state and symbol. His model became known as the “Turing machine“.

The Church-Turing thesis states that everything that can be computed can also be computed by a Turing machine. In other words, there isn’t any computational device more powerful than a Turing machine. A computational system is considered Turing complete if it can simulate this machine and thus perform any possible computation.

Examples of Turing complete systems abound in computer science, from programming languages like Python and Java to cellular automata like Conway’s Game of Life and even some games and puzzles like Minesweeper.

Origami’s Computational Prowess

In their groundbreaking work, Zakharevich and Hull proved origami’s Turing completeness by showing how to encode computational elements within the intricate folds of paper. They designed crease patterns that specified where and how to fold the paper to perform logical operations.

Here’s how it works: pleats in the paper represent Boolean signals traveling in a given direction. The orientation of the pleat after folding indicates a value of 0 or 1 (or TRUE or FALSE).

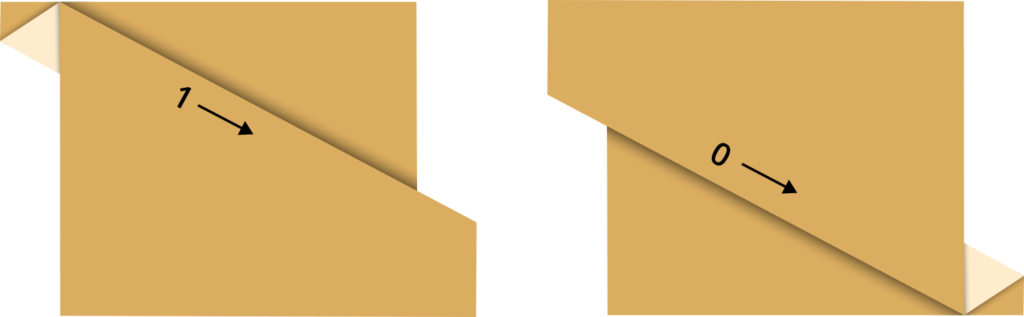
At the points where two signals meet, logic gates or gadgets are created to determine the outcome of their interaction. These gadgets can then be combined to create increasingly complex computational circuits.

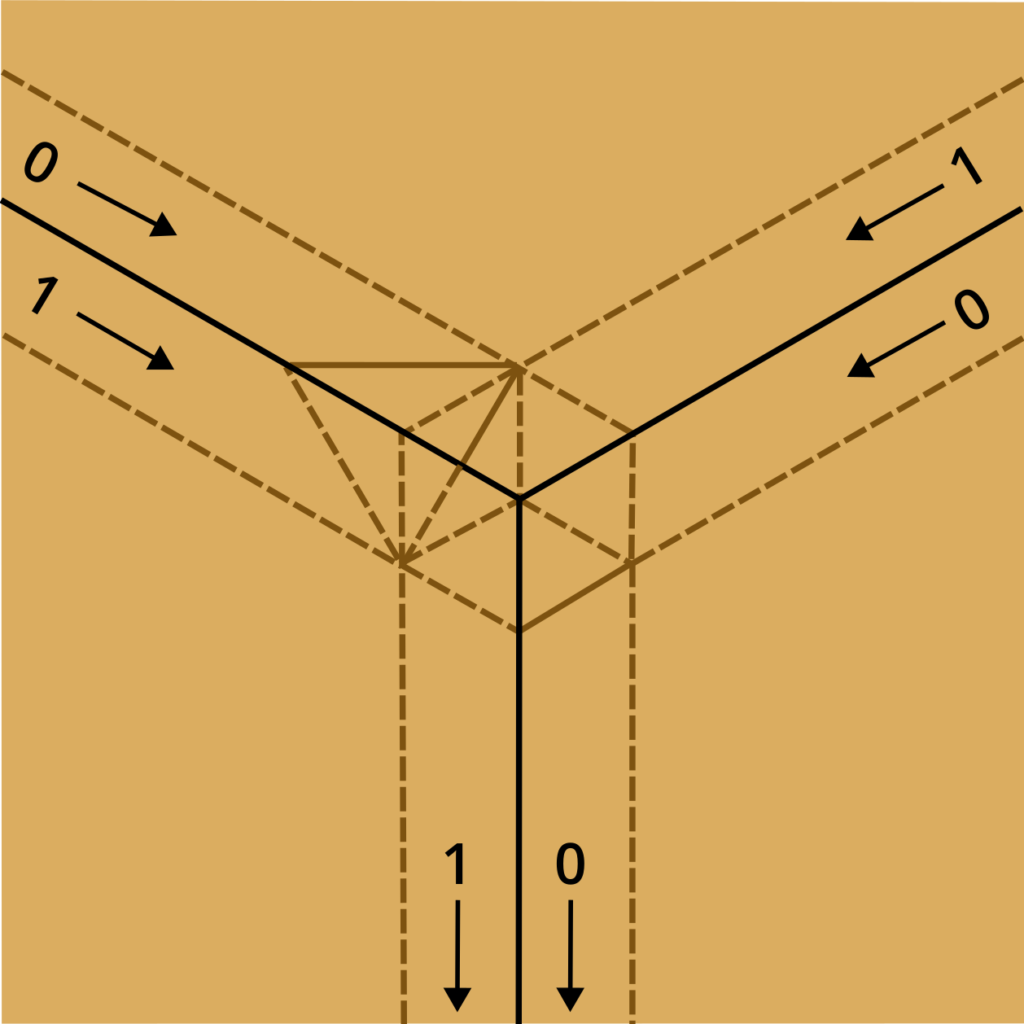
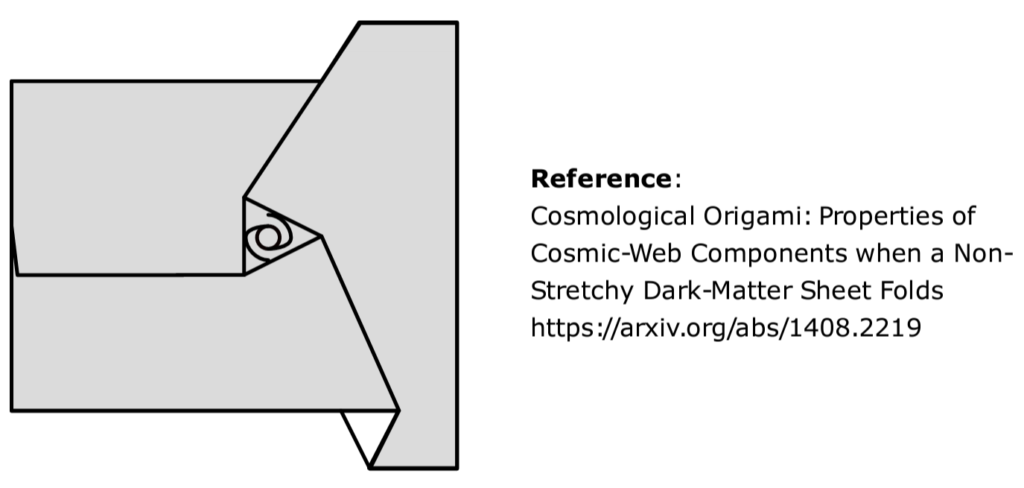
All folds are performed on a triangular grid, and the figure below shows the crease pattern for an AND gate (the output is 1 if and only if both inputs are 1).

Here are two different foldings of the AND gate:

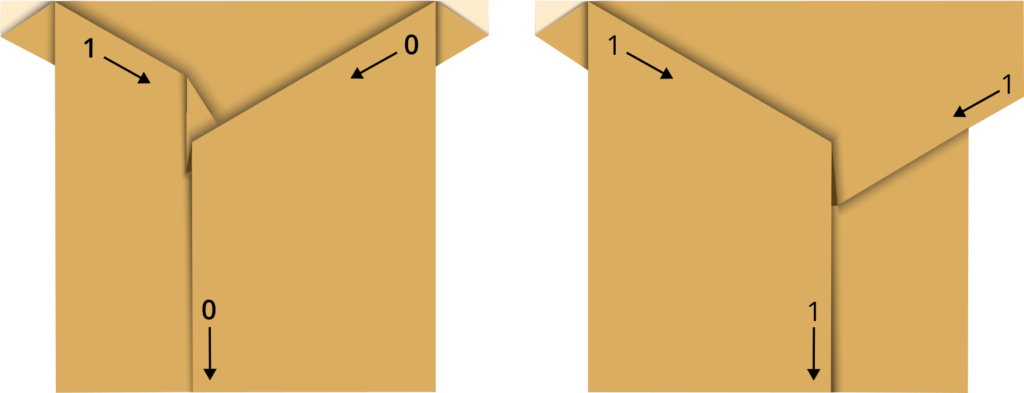
In their paper, you can find crease patterns for other gates like OR, NAND, NOR, and NOT, as well as gadgets for splitting signals, intersections, and signal “eaters.”

Through this ingenious approach, Zakharevich and Hull showed how to build an origami circuit that simulates Rule 110, a one-dimensional cellular automaton already known to be Turing complete.

Implications: From Theory to Practice

The revelation that origami is Turing complete carries profound implications for both theoretical and practical domains. On the theoretical front, it reinforces the universality of computational principles, demonstrating that computation is not limited to electronic devices or abstract mathematical constructs but can also be achieved through physical manipulations of paper.

This discovery expands the scope of computational theory and provides a new medium through which to explore algorithmic processes. It also contributes to the ongoing dialogue about the nature of computation and the limits of computability, challenging traditional notions of what constitutes a computing device.

In practical terms, the applications of computational origami are vast and varied. In education, for instance, origami could serve as a hands-on tool for teaching computational concepts. By folding paper to perform logical operations and simulate algorithms, students can gain a tangible understanding of abstract principles, making learning more interactive and accessible.

In technology and design, the principles of computational origami could inspire innovative solutions and products. Foldable structures that mimic computational processes could lead to advancements in robotics, materials science, and architectural design. The ability to encode and manipulate information through folds opens up new possibilities for creating adaptive and efficient systems.

Build Your Own Origami Computer

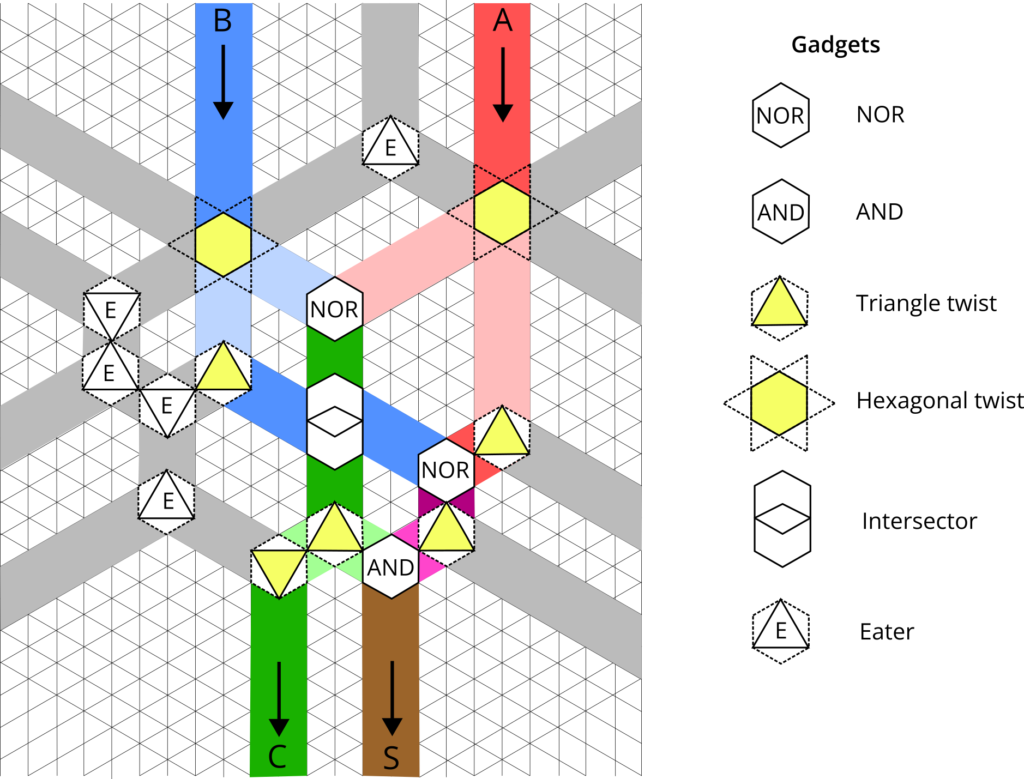
While building a full-fledged origami computer might seem daunting, constructing simple logic circuits is a fascinating and achievable endeavor. I took a shot at building a digital half-adder circuit, which can add two single-bit binary numbers. Its operation is represented by the following truth table:

A	B	C	S
0	0	0	0
0	1	0	1
1	0	0	1
1	1	1	0

The half-adder circuit follows these equations:

C = A AND B,
S = (A OR B) AND NOT C.

When implementing the equations into an origami circuit, those equations require a bit of tweaking. You’ll need to split the signals and direct them toward the logical gates, but the gadgets for signal splitting invert the value at the output. For instance, I computed the output C using this equivalent expression:

C = ((NOT A) NOR (NOT B)).

In the image below, you can see the resultant crease pattern. The gadget symbols follow the same convention and meaning as in Zakharevich and Hull’s paper.

If you’re up for a challenge, try your hand at building a XOR gate (which will allow for a simpler half-adder circuit), a 2-bit adder, or a flip-flop.

Cosmic Origami: The Universe as a Folded Computer?

Now, let’s indulge our imaginations for a moment. The folding mechanisms proposed by Zakharevich and Hull bear a striking resemblance to the cosmic origami model developed by Dr. Mark Neyrinck at University of Denver. In this model, the universe’s structure can be seen as a web of galaxies, clusters, and voids, shaped by the underlying distribution of dark matter. The signals and gates of the origami computer would correspond to the filaments and nodes of galaxies in the origami cosmos.

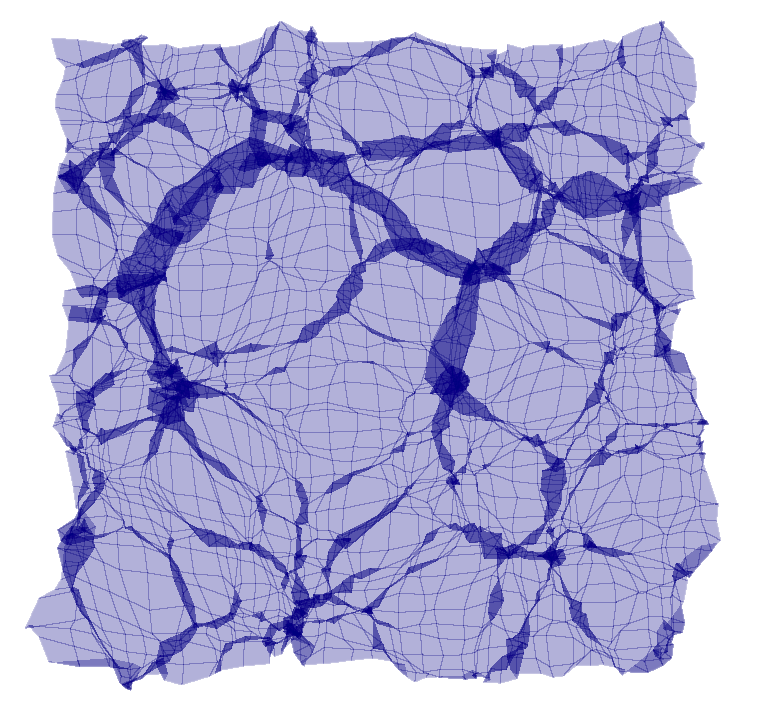
Compare, for example, the folded AND gate above with the origami galaxy model by Dr. Neyrinck:

While the origami computer exists as a 2D sheet folded in a 3D space, the origami cosmos is created by a 3D “sheet” of dark matter folded in a 6D space, making it far more complex. Yet, the similarity is undeniable, and it invites speculation: if the principles of origami can encode computations, could the universe itself be viewed as a vast computational entity?

This idea aligns with some of the most provocative theories in cosmology, like Max Tegmark’s Computable Universe Hypothesis (CUH), which posits that the universe is not just described by mathematics but is a mathematical structure composed of computable functions. If this is the case, then the universe operates like a gigantic computer, processing information according to mathematical rules.

So, what is our role, as intelligent beings, in this cosmic computation? Are we mere players in an elaborate simulation, like in the Matrix movies? Or perhaps, life itself is a software bug in the grand scheme of things? These mind-bending questions might provide inspiration for the next great sci-fi author. (Who knows, maybe the answer lies in a well-folded piece of paper!)

Conclusion: Embracing the Unexpected

Origami’s Turing completeness is a testament to the power of interdisciplinary exploration and a reminder that the boundaries between art and science are often blurred. By bridging the tactile world of paper folds and the abstract domain of computational theory, this groundbreaking research invites us to reconsider the very nature of computation.

It underscores that computation is a universal language, capable of being expressed through various mediums, whether silicon chips or sheets of paper. The concept of origami’s Turing completeness celebrates the elegance and power of combining diverse fields, reminding us that creativity and logic are not mutually exclusive but can together lead to profound insights and breakthroughs.

As we continue to explore the possibilities of computational origami, we embrace a future where the boundaries of art, science, and technology blur, leading to endless potential for discovery and innovation. Perhaps the next great computational breakthrough will come not from a high-tech laboratory but from the simple fold of a piece of paper, reminding us to keep an open mind and embrace the unexpected.

So, let’s fold, crease, and compute our way to a future where the lines between art and science are blurred, and where the only limit is the boundless creativity of the human mind. Who knows what other ancient practices might hold the keys to unlocking the mysteries of the universe? The possibilities are as limitless as the folds we can create.